Die „Martyrer Enderklärung“ verstehen Ihre lange Artikelschrift im formellen Deutsch über die „Martyrer Enderklärung“ kann mit dieser Struktur aufgebaut werden:
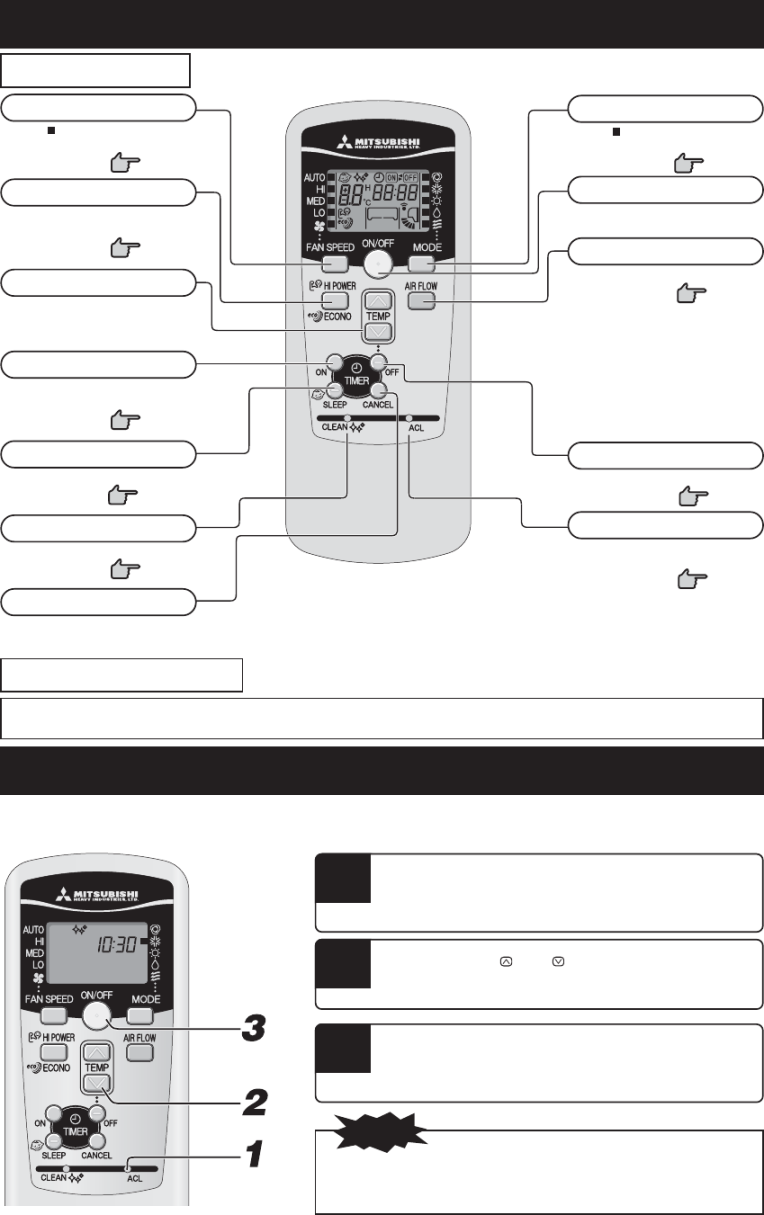
Mitsubishi Klimaanlage Fernbedienung Symbole Erklärung Die Steuerung Ihrer Mitsubishi-Klimaanlage erfolgt bequem über die Fernbedienung. Verschiedene Symbole auf der Fernbedienung bieten
Motortypenschild Erklärung Ein Motortypenschild ist ein kleines Schild oder Aufkleber, das direkt am Motor angebracht ist und wichtige Informationen über
Opel Vivaro Kontrollleuchten Erklärung Die Kontrollleuchten im Armaturenbrett Ihres Opel Vivaro dienen dazu, den Fahrer über den Zustand wichtiger Fahrzeugsysteme
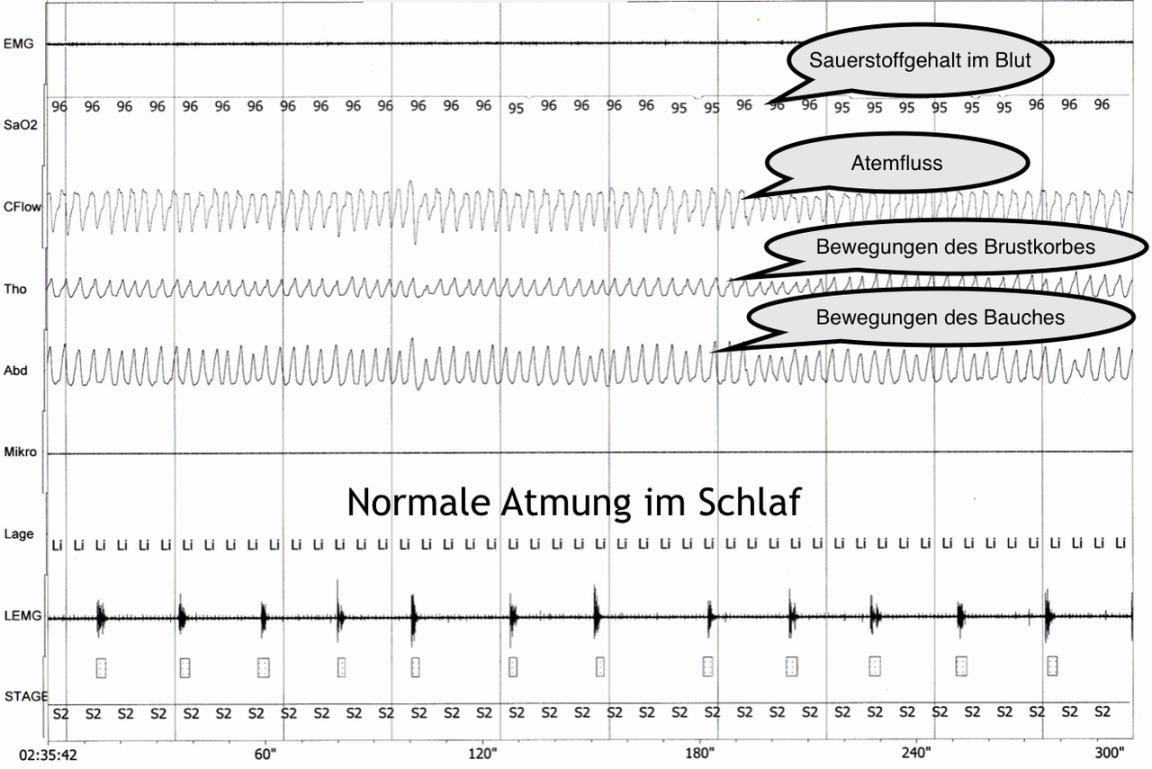
Polygraphiebefund Erklärung Ein Polygraphiebefund ist die Ergebniszusammenfassung einer Polysomnographie, einer Untersuchung, die während des Schlafes durchgeführt wird, um Schlafstörungen und
Spanngurt Etikett Erklärung Ein Spanngurt, auch Zurrgurt genannt, ist ein Gurtband, das zum Sichern von Ladung auf Paletten, Anhängern oder
Arten von Mord (Kinds of Murder) und deren strafrechtliche Einordnung (Legal Classification) Der Begriff „Mord“ umfasst im Strafrecht nicht einfach